看到大多数计算最大回撤的代码都是 $O(n^{2})$ 的算法复杂度,其实最大回撤的计算用 $O(n)$ 的算法复杂度就能实现,只需对 $O(n^{2})$ 复杂度的代码稍作修改即可。
我们先来回顾下最大回撤的定义:
$最大回撤 = max(1-策略当日价值/当日之前账户最高价值)$
我们来生成一个数组,包含连续1000个时间点的账户价值
import matplotlib.pyplot as plt
import numpy as np
np.random.seed(1)
a = np.random.randn(1000)
values = np.cumsum(a)
plt.plot(values)
plt.show()
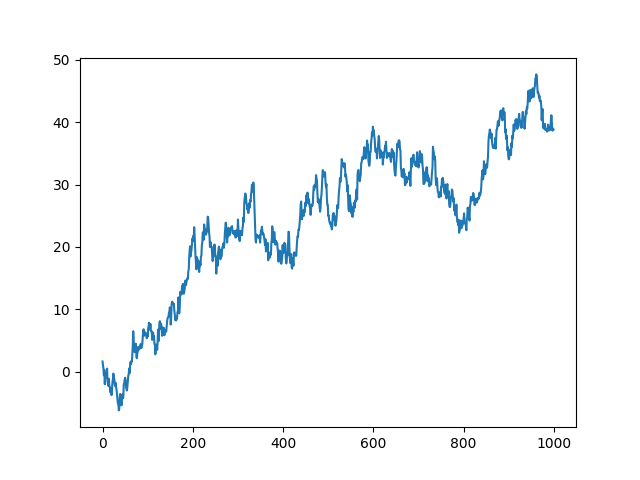
上述1000个时间点的账户价值画出来的资金曲线是这样的
$O(n^{2})$ 的实现方式
对于这样一个账户价值的序列计算最大回撤,通常的实现方式是这样的
def get_max_drawdown_slow(array):
drawdowns = []
for i in range(len(array)):
max_array = max(array[:i+1])
drawdown = max_array - array[i]
drawdowns.append(drawdown)
return max(drawdowns)
最外层的循环遍历数组中所有的元素。对于array中的每个元素array[i],找到这个元素之前所有元素的最大值:max_array = max(array[:i+1]),然后max_array - array[i]就代表了以i为截止点的所有回撤的最大值,把max_array加入数据drawdowns数组中。最大回撤就是drawdowns的最大值。
求最大值的复杂度是 $O(n)$,所以max(drawdowns)的复杂度 $O(n)$,每一次循环中计算max(array[:i+1])的复杂度是 $O(i+1)$, 所以总的算法复杂度是 $O(n^{2})$ 。
$O(n)$ 的实现方式
上述代码中,每次循环里面我们都计算max(array[:i+1]),相当于每次我们都遍历前i+1个数来求最大值。但其实
$前i + 1个数的最大值 = max(前i个数的最大值,第i + 1个数)$
用动态规划改进我们的代码。每次循环我们把迄今为止的最大值记下来,下次循环只需将当前元素值和之前记录的最大值比较一下,就能求得新的最大值。
改进后的代码如下:
def get_max_drawdown_fast(array):
drawdowns = []
max_so_far = array[0]
for i in range(len(array)):
if array[i] > max_so_far:
drawdown = 0
drawdowns.append(drawdown)
max_so_far = array[i]
else:
drawdown = max_so_far - array[i]
drawdowns.append(drawdown)
return max(drawdowns)
max_so_far记录当前遍历过的元素的最大值,并被不断更新。每次计算最大值不再需要遍历之前的所有元素,只要比较max_so_far和array[i]即可。比较两个数值的复杂度是 $O(1)$,所以总的复杂度是 $O(n)$。
性能测试
我们来测试一下上面两个算法的性能
import timeit
print timeit.timeit('get_max_drawdown_slow(values)', setup="from __main__ import get_max_drawdown_slow, values", number=100)
print timeit.timeit('get_max_drawdown_fast(values)', setup="from __main__ import get_max_drawdown_fast, values", number=100)
每个函数运行100次,计算总时间,结果如下
2.69495010376
0.0435910224915
可以看到 $O(n)$ 算法有60倍的性能提升。
附:完整的源代码
import timeit
import matplotlib.pyplot as plt
import numpy as np
def get_max_drawdown_slow(array):
drawdowns = []
for i in range(len(array)):
max_array = max(array[:i+1])
drawdown = max_array - array[i]
drawdowns.append(drawdown)
return max(drawdowns)
def get_max_drawdown_fast(array):
drawdowns = []
max_so_far = array[0]
for i in range(len(array)):
if array[i] > max_so_far:
drawdown = 0
drawdowns.append(drawdown)
max_so_far = array[i]
else:
drawdown = max_so_far - array[i]
drawdowns.append(drawdown)
return max(drawdowns)
np.random.seed(1)
a = np.random.randn(1000)
values = np.cumsum(a)
print timeit.timeit('get_max_drawdown_slow(values)', setup="from __main__ import get_max_drawdown_slow, values", number=100)
print timeit.timeit('get_max_drawdown_fast(values)', setup="from __main__ import get_max_drawdown_fast, values", number=100)
print get_max_drawdown_slow(values)
print get_max_drawdown_fast(values)
plt.plot(values)
plt.show()