Numpy中有一个非常方便的特性:broadcasting。当我们对两个不同长度的numpy数组作二元计算(如相加,相乘)的时候,broadcasting就在背后默默地工作。本文我们就来介绍下numpy的broadcasting。
什么是broadcasting
我们通过一个简单的例子来认识一下broadcasting,考虑下面的代码
import numpy as np
a = np.array([0, 1, 2])
b = np.array([5, 5, 5])
c = a + b
a+b其实是把数组a和数组b中同样位置的每对元素相加。这里a和b是相同长度的数组。
那如果是不同长度的数组呢?考虑下面的情况
d = a + 5
这里就用到了broadcasting。broadcasting会把5扩展成[5, 5, 5],然后上面的代码就变成了对两个同样长度的数组相加。用图画出来,是这样的一个过程(半透明的方块表示被扩展出来的数值)

需要注意的是,broadcasting不会分配额外的内存来存取被复制的数据,这里为了描述方便作了简化。
接下来我们扩展一下上面的例子,看一下多维数组的情况
e = np.ones((3, 3))
# e is
# array(
# [[ 1., 1., 1.],
# [ 1., 1., 1.],
# [ 1., 1., 1.]])
e + a
# array([
# [ 1., 2., 3.],
# [ 1., 2., 3.],
# [ 1., 2., 3.]])
这里一维数组a被扩展成了二维数组,和e的shape相同。用图的形式表示,是这样的
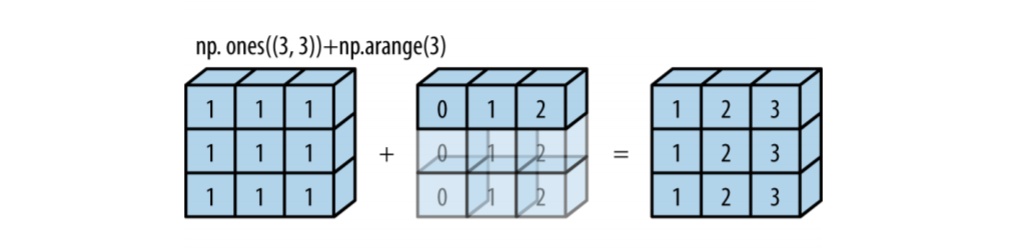
我们再来考虑一个更复杂的情况,需要对两个数组都做broadcasting的例子
b = np.arange(3).reshape((3, 1))
# b is
# array([
# [0],
# [1],
# [2]])
b + a
# array([
# [0, 1, 2],
# [1, 2, 3],
# [2, 3, 4]])
这里a和b都被扩展成相同shape的二维数组。用图的形式表示这个过程,如下
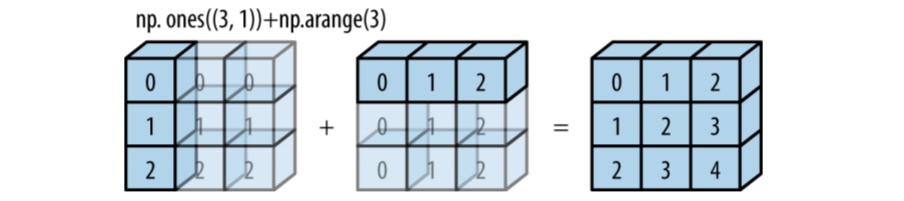
broadcasting的规则
对两个numpy数组之间的作二元计算,broadcasting须遵循一下规则:
-
- 如果两个数组维数不相等,维数较低的数组的shape会从左开始填充1,直到和高维数组的维数匹配
-
- 如果两个数组维数相同,但某些维度的长度不同,那么长度为1的维度会被扩展,和另一数组的同维度的长度匹配
-
- 如果两个数组维数相同,但有任一维度的长度不同且不为1,则报错
我们来举例说明一下上面的规则
例1
a = np.arange(3)
b = np.ones((2, 3))
这两个数组的shape分别是
a.shape = (3,)
b.shape = (2, 3)
对这两个数组作二元计算,根据规则1,数组会被填充成
a.shape -> (1, 3)
b.shape -> (2, 3)
根据规则2,第一个维度不等,所以我们对维度作扩展
a.shape -> (2, 3)
b.shape -> (2, 3)
现在两个数组的shape一致了,可以相加得到下面的结果
a + b
# array([
# [ 1., 2., 3.],
# [ 1., 2., 3.]])
例2
a = np.arange(3).reshape((3, 1))
b = np.arange(3)
两个数组的shape分别是
a.shape = (3, 1)
b.shape = (3,)
根据规则1,b的shape要被填充
a.shape -> (3, 1)
b.shape -> (1, 3)
根据规则2,维数相等,但维度内的长度不等,所以需要进一步扩展
a.shape -> (3, 3)
b.shape -> (3, 3)
现在两者shape一致了,作相加计算可以得到如下结果
a + b
# array([
# [0, 1, 2],
# [1, 2, 3],
# [2, 3, 4]])
例3
我们再来看一个broadcasting报错的例子
b = np.ones((3, 2))
a = np.arange(3)
两个数组的shape分别是
b.shape = (3, 2)
a.shape = (3,)
根据规则1,a的shape会被填充
b.shape -> (3, 2)
a.shape -> (1, 3)
根据规则2,数组a的第一个维度会被扩展
b.shape -> (3, 2)
a.shape -> (3, 3)
这里我们满足规则3的条件了,维数相等,但第二个维度的长度不等,且不为1,因此这两个数组相加会报错,如下
b + a
# output
ValueError Traceback (most recent call last)
<ipython-input-30-15a3d2288d92> in <module>()
----> 1 b + a
ValueError: operands could not be broadcast together with shapes (3,2) (3,)
总结
broadcasting在numpy数组的计算中无处不在,任何二元运算的ufunc都实现了broadcasting机制。broadcasting也很方便,很多时候我们甚至感知不到它的存在,但深入地理解它背后的工作机制,可以帮助我们避开一些陷阱。